Algoritmo de la división y Regla de Ruffini

 

    Durante el desarrollo en el colegio se adquieren conocimientos que luego serán de gran beneficio para el futuro. En el área de la matemática se aprende sobre temas relacionados con la geometría, el algebra y la estadística. Todos estos de gran importancia para el desarrollo de la vida. Aquí, se explicará uno de los temas que muchos estudiantes ven al prepararse para la universidad en la materia de matemáticas. El tema es la división de polinomios.

    Más adelante se explicará cómo realizar la forma de hacer el algoritmo de la división, pero ahora se hablará un poco acerca de la regla de Ruffini. Esta regla es un método matemático que hace más sencilla y rápida la división de polinomios. La regla de Ruffini fue inventada por el filósofo matemático Paolo Ruffini. Paolo nació a mediados del siglo XVIII y falleció a inicios del XIV. (Aznar, 2007, parr. 1.) 

    De la misma manera, Ruffini llegó a desarrollarse en varios campos durante su vida en Módena. Él estudió matemática, filosofía, medicina y literatura. Paolo fue médico y rector de una Universidad durante un periodo de su vida. Escribió sobre filosofía. Para finalizar, Paolo Ruffini fue destacado por sus diversos aportes en la matemática. (Aznar, 2007.)

División de Polinomios

    Para comprender bien el concepto y la función de la división de polinomios, se debe iniciar con entender qué es un monomio. Un monomio es un término algebraico, donde cada variable tiene un exponente entero positivo. (pimás, 2016.) Un ejemplo sería, "2x" o bien "8zmy". 

Fuente: Elaboración propia.

Ahora bien, un polinomio es la suma o resta de dos o más monomios no semejantes. (pimás, 2016) Para una mejor comprensión se desarrollará un ejercio como ejemplo.

Ejemplo: 

 p(x)=  

q(x)=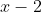  

Hay que buscar c(x) y r(x). 

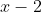En otras palabras, el dividendo es "" y el divisor es "" y se busca el cociente y el residuo.

Nota: para cualquier ejercico de división se deben incluir "0"(ceros) de guía cuando un grado del polinomio no está expresado. En este ejercicio, el grado uno no está expresado por lo que se pone un cero para evitar errores durante el ejercicio.

Se debe colocar el formato de división común, como se observa de la siguiente manera.

Seguidamente, para realizar la división se deben cumplir una serie de pasos.

1.) En primer lugar, hay que pensar en un número que al multiplicarlo por el "1"que acompaña la "x" del divsor de como resultado "8". Ese número sería el mismo "8". 

Luego, este valor se coloca debajo del de la linea del divisor y el resultado debajo del dividendo con el símbolo contrario. Esto de la forma a continuación.

     

2.) Después se debe de buscar un valor que al multiplicarlo por la "x" del divisor de como producto "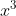". Ese valor sería "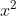". Y se colocarían de la siguiente forma. 

3.) Lo siguiente por hacer es multiplicar el valor "" por cada monomio en el divisor, que en este caso sería solo el "-2". Quedando como se muestra.

               

4.) El siguiente paso es realizar una resta, el primer valor que es "" se cancela, es decir da "0" por lo que la resta sería del "" y del "".

5.) Ahora se repite el paso 1 y 2, pero ahora buscando un "". Y así sucesivamente hasta llegar a un valor que sea menor al grado del polinomio del divisor. Este valor que sobre será el residuo de la división. Ahora, la división terminaría algo así:

Ahora ya concluido el ejercicio, el cosiente, c(x)=  y el residuo, r(x)= 61.

Regla de Ruffini

Con se mencionó anteriormente, la regla de Ruffini es un método matemático utilizado para hacer la división entre polinomios. Esta es un caso similar al método de la división sintética. A continuación se explicará como realizarla. 

Ejemplo: 

1.) Para desarrollar la regla de Ruffini se debe tomar en cuenta que solo funciona con la forma "mx+b" donde "m" es "1" y el "b" es un número natural. Para este método se untiliza la fórmula . Y de acuerdo a este ejercio sería , dando como resultado 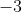. (Gamboa, M. E., 2015 )

2.) Seguidamente se colocan cada valor del dividendo y el número "-3" de la siguiente manera.

Nota: para cualquier ejercico de división se deben incluir "0"(ceros) de guía cuando un grado del polinomio no está expresado. Es decir si se tiene "" los número que se escribiría en la parte superior serían "4, 0, 0, 6". Esto debido a que en el binomio mostrado de ejemplo no poseen valores de grado 2 ni de grado 1, y si no se utilizan los ceros existe la posibilidad de fallar el ejercicio.

3.) El primer número en el diagrama se baja y se coloca de la siguiente manera.

4.) Ahora, se multiplica el "-3" por el "10" y se coloca debajo del "-2" se realiza una suma y el resultado se pone a la par del 10, y así con el resto de los números.

La figura anterior muestra la forma de resolver la división entre "" y "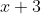" mediante la fórmula de Ruffini. Algunos se preguntarán dónde está el residuo y el cociente. El residuo de esta división es el número que se encuentra en el recuadro verde. En cuanto al cociente, este se complementará con los números "10" y "-32". Además de estos valores, se debe colocar las variables correspondientes. En fin, el cociente sería "10x -32".

  

        A modo de cierre, ambos métodos explicados son de gran ayuda para la división de polinomios. Es de gran interés el conocer sobre la vida de matemáticos, así como lo fue Paolo Ruffini. De igual forma, es muy importante el conocer y entender muy bien ambos métodos expuestos, ya que este conocimiento se puede aplicar en futuros temas de estudio.  

Referencias

Aznar, E. R. (2007). Paolo Ruffini Matemático y médico (1765 Valentano, 1822 Módena, actualmente Italia). Recuperado de https://www.ugr.es/~eaznar/ruffini.htm

Gamboa, M. E. (2015).  Alternativa didáctica para la división entera de polinomios.

Gómez, L. A. (Ed.). (2016). Matemática 8 DESARROLLANDO HABILIDADES. pimás.